Les principes de validation des données ont été récemment appliqués avec succès à un projet de rétro-ingénierie ferroviaire. B et ProB ont démontré une fois de plus leur efficacité lorsqu’ils sont utilisés en combinaison.
Ce projet visait à redévelopper un IDE pour les systèmes de diagnostic embarqués (EDS), principalement à partir de zéro car le code source et la documentation de développement ont été perdus. Le matériel obsolète (sans accès direct au système de fichiers) et l’IDE d’origine ont été utilisés pour les tests en boîte noire.
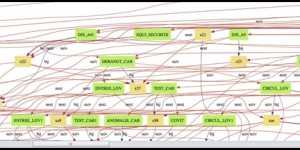
Une vaste collection d’exemples a été conçue et saisie, dans l’ordre :
- collecter les fichiers binaires générés,
- deviner la structure des fichiers,
- déterminer les règles de compilation, avec pour seul support le code assembleur 68k de l’interpréteur du langage cible, puisque le code binaire et les instructions sont spécifiques à cette application.
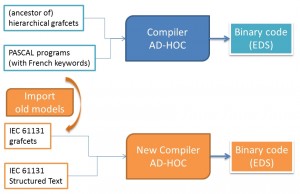
De plus, les deux langages d’entrée utilisés par l’IDE original, l’ancêtre des grafcets hiérarchiques et le Pascal avec des mots-clés français, sont anciens et non standardisés. Une étape supplémentaire a consisté à définir deux nouveaux langages, basés sur la norme IEC 61131-3, qui seraient supportés par le nouvel IDE, et à fournir des moyens d’importer des programmes originaux dans le nouvel IDE.
La contrainte ultime était de pouvoir compiler les programmes de manière à ce que les binaires résultants soient bituellement identiques à ceux obtenus à partir de l’IDE d’origine. L’application cible utilisée pour la validation fait environ 800k octets.
Après plusieurs opérations de rétro-ingénierie, il est apparu que le fichier binaire était composé de plusieurs « composants » tels que des grafcets, des programmes, des procédures, etc. mais sans table de symboles et donc sans moyen direct de détecter l’ordre de compilation requis. Afin de retrouver cet ordre, il a été décidé de se concentrer sur l’ordre d’exécution des grafcets et des sous-grafcets.
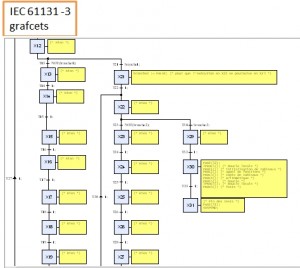
Une application EDS consiste à naviguer dans des grafcets hiérarchiques : un état actif d’un grafcet peut activer un sous-grafcet (un grafcet enfant) tant que cet état reste actif. Ainsi, du côté du programme, les relations entre les grafcets sont connues (la relation parent-enfant est un graphe acyclique dirigé). Du côté binaire, les instructions d’activation des grafcets peuvent être analysées et associées à un grafcet, de sorte qu’un autre graphe acyclique dirigé peut être construit. Le problème principal est que nous ne savons pas facilement comment associer l’état du grafcet d’un graphe à la référence du code binaire de l’autre graphe, à l’exception de la racine des graphes. Chaque graphe est composé de plus de 160 nœuds et la recherche de la solution nécessiterait beaucoup de calculs.
Ce problème a été résolu de manière élégante en utilisant les principes de validation des données : un modèle B représentant les deux graphes et leurs propriétés a été élaboré, et ProB a été utilisé pour trouver une solution.
Du côté de la modélisation des grafcets, G7 représente l’ensemble des grafcets apparaissant dans le projet
G7 = {main, G1, G2, G3, G4, …. }
et next est la relation associant à un grafcet ses enfants.
next: G7 <-> G7
next = { …, G7 |-> G11, …}
Du côté du fichier binaire, ADR représente l’ensemble des entités (grafcet, programme, etc.) apparaissant dans le projet (en fait leur « adresse »).
ADR = {0x01, 0x13, 0x15, …}
et suiv est la relation associant à une entité les autres entités appelées.
suiv: ADR <-> ADR
suiv = { … , 0x10 |-> 0x15, …}
La propriété recherchée était la suivante : « Les sous-grafcets appelés dans le fichier binaire doivent être conformes aux sous-grafcets activés dans les modèles d’entrée ». Il existe une bijection bij qui associe à un nœud de G7 un nœud de ADR de telle sorte que les enfants des deux nœuds correspondent.
La propriété est exprimée dans B comme suit :
bij: G7 >->> ADR &!xx.(xx: G7 => bij[next[{xx}]] = suiv[bij[{xx}]])
ProB a réussi à trouver la solution (en fait les deux solutions … ) en moins de 10 secondes. Le graphe de correspondance obtenu est le suivant :
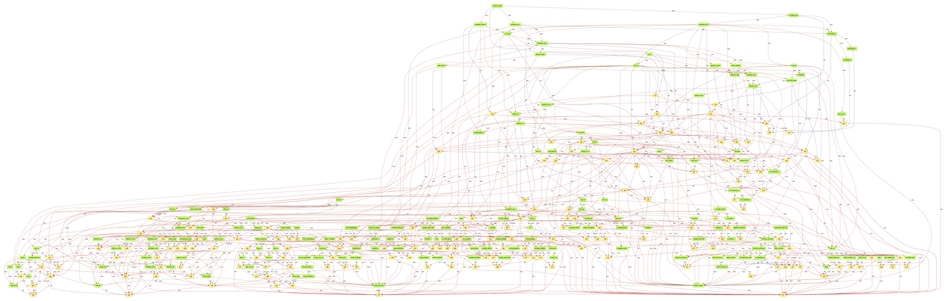
Il apparaît finalement que :
- les graphes ne sont pas acycliques (il existe des boucles qui sont de véritables bogues)
- certains sous-graphes sont déclarés mais jamais activés (code mort)