Vérification système avec preuve pour le CBTC de la ligne 7 (Flushing), New York

CLEARSY a procédé à la vérification système avec preuve du CBTC de la ligne 7 de New York, avec la méthode B. La vérification formelle obtenue est un élément de la démonstration de sûreté de fonctionnement, très importante pour la validation d’un tel système ferroviaire critique.

• CLIENT : New York City Transit (NYCT)
• LIEU : New York – USA
• DATE : 2011 à 2013

Contexte

Dans le cadre de la modernisation de son réseau de transport ferroviaire, New York City Transit a confié à THALES Toronto la réalisation d’un CBTC pour la ligne 7 (Flushing).

Ce système permettra d’optimiser en toute sécurité le pilotage des trains par la réduction de leur espacement et bénéficier ainsi d’une capacité de transport accrue, avec un gain supplémentaire consistant à réduire les équipements de voie (Circuits de voies et signaux).

Le CBTC se compose d’une partie bord (Embarquée sur des rames R142 modifiées) et une partie sol (Contrôleurs de zone et superviseur central). il s’interface avec le système de routes, de feux d’aiguilles existant (Modifié spécifiquement).

Notre expertise

NYCT a souhaité obtenir une garantie par preuve de la sécurité du système CBTC pour Flushing. pour le démontrer, CLEARSY a réalisé une preuve système avec la méthode formelle B.

les propriétés systèmes prouvées sont :

• L’impossibilité de collision entre trains
• L’impossibilité de déraillement sur aiguille déverrouillée
• L’impossibilité de survitesse

Nos actions

CLEARSY a utilisé dans son mode opératoire la description détaillée de la conception et des algorithmes employés par THALES pour le CBTC de Flushing : nous avons par exemple utilisé (et modélisé) les éléments suivants :

• comptage des impulsions des tachymètres (et particularités si changement de direction / glissements)
• filtrages (Kalman) pour la mesure de vitesse
• prise en compte des pentes pendant les phases d’établissement de freinage pour le modèle de freinage
• communication bord / sol : détermination des dates de messages, croisements de messages, systèmes de timeout
• échanges de suspicion de matériel non communicant entre contrôleurs de zones
• dépassements des signaux par les trains manuels, enclenchements et provisions en cas de changements de modes ou retournements
• destructions d’itinéraires et échanges filaires avec l’interlocking sur les approches.

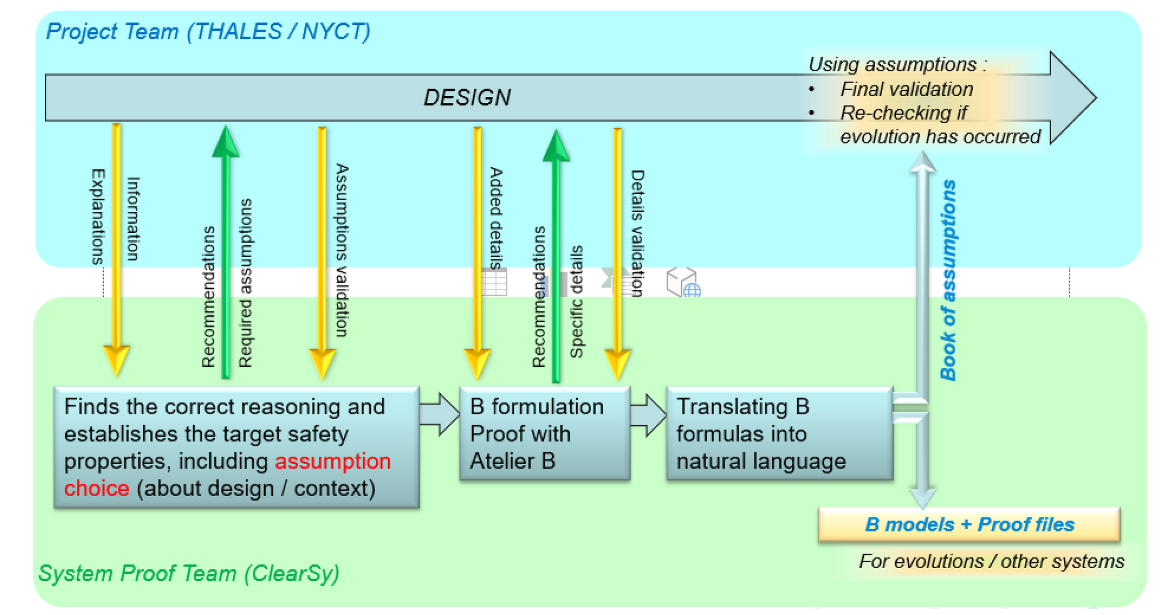
Les modèles B ainsi obtenus contiennent la formulation mathématique des propriétés voulues, la formulation mathématique de toutes les hypothèses nécessaires et les éléments de conduite de preuve. Une fois ces modèles prouvés avec l’Atelier B, nous avions donc la garantie que les propriétés voulues découlaient mathématiquement des hypothèses sélectionnées.

Ces hypothèses constituent donc toutes les conditions suffisantes pour garantir logiquement les propriétés voulues. Ces conditions concernent la conception, le matériel et le contexte : tout ce qui n’est pas purement mathématique doit être introduit pour que le prouveur automatique puisse aboutir.

Ces conditions ont été choisies au fil de l’eau de l’étude avec la collaboration suivie de NYCT et THALES, afin d’obtenir des conditions réalistes avec la conception et d’interagir avec cette conception suffisamment tôt (sous forme de recommandations).

À la fin du projet, nous sommes partis de la formalisation B de ces hypothèses pour obtenir une rédaction très précise de ces conditions. Elles peuvent ainsi être confirmées avant la mise en service et restent vérifiables lors de toute évolution / changement du système. Nous avons donc livré les documents détaillés et validés décrivant de manière compréhensible et vérifiable l’ensemble des conditions suffisantes pour que les propriétés voulues soient mathématiquement garanties.

Pour les parties logicielles, les conditions obtenues définissent des lois que le logiciel doit satisfaire. Ainsi la preuve système produit des validations précises à faire sur le logiciel, tout en restant indépendante du codage.

En résumé, ce projet implémente l’idée que la preuve mathématique des propriétés de sécurité d’un système (quelle que soit sa taille) peut être conduite lors de sa conception, à un niveau de détail défini par les hypothèses choisies. La preuve mathématique outillée avec l’Atelier B devient alors applicable. Notons que ce processus nécessite la compréhension fine du véritable « pourquoi » de la sécurité, obligeant ainsi des échanges forts avec les experts métiers concernés. Mais ces échanges en vue d’une preuve constituent déjà un apport en soi.